
저자 : 궤도
출판 : 동아시아
출간 : 2022.10.17
이 도서는 출판사로부터 제공받았습니다
과학도에게 세상은 극소수의 옳은 것과 다수의 옳지 않은 것들로 이루어진다. 하지만 not A가 확정적으로 옳지 않은 것이 되는 순간은 가변적이다. 과학이란 학문이 최초의 발생 이후 수많은 단계를 거쳐 '발전'해왔다는 이미지는 또 하나의 환상이라고 생각된다. 우리는 한 계단씩 걸어 올라가고 있는 것이 아니라, 매번 한 줌의 모래를 움켜쥔 다음 조건에 맞는 것들을 골라내고 있을 뿐인지도 모른다.
옳은 것을 '알고' 있는 자와 그외의 것들을 '믿는' 자들은 과학계에서 외부를 바라볼 때 흔히 존재하는 시각이다. 다만 그 '알고 있음'이 관측 시점에 따라 '믿는' 것과 다르지 않은 순간이 발생한다는 점과, 때때로 새로운 '앎'은 이전까지 부숴왔던 옳지 않음을 다시금 옮음의 위치로 옮겨놓는다는 점이 문제다.
그러나 자신이 옳다고 생각하는 것을 자신만의 논리로 검증하고 고찰하는 자와 생각 없이 받아들이는 자 사이의 차이는 틀림없이 존재하므로, 나는 일반적인 대중 과학의 의의는 '자신의 생각을 한계까지 정제하는 법'을 내재화하는 법을 익히는 데 있다고 생각한다. 진정한 "과학이 필요한 시간"이란 당황스럽지 않게, 목적에 맞게 상황과 조건을 고려한 선택을 내릴 수 있도록 관찰하고 결론짓는 '매일의 일상'인 것이다.
기본적으로 과학은 현상의 관찰에서 출발한다. 그를 통해 쌓은 정보들로 가설을 수립하고, 그것이 충분히 개연성 있게 재연될 때 가설과 추측은 하나의 이론으로 자리 잡는다. 그 이론이 정설로 받아들여지는 것은 또 다른 이야기이다. 가설들이 쌓이면 추론을 통해 현상을 특정하고 관측해냄으로써 새로운 이론을 증명하는 연역적 접근을 하기도 하지만, 자연 과학의 경우 대부분은 현상이 먼저다.
궤도 저자의 신작 <과학이 필요한 시간>은 이렇게 일상적인 상황이나 현상에서부터 비롯되는 의문을 거대 블랙홀과 시간, 양자의 세계까지 풀어나간다. 무엇보다 그의 재치있는 입담과 유머가 유감없이 발휘되었으므로 어려울 것 같다는 걱정은 내려놓고 신나게 즐겨보시길.
이 책은 다양한 지식과 흥미로운 과학/수학사의 비하인드들을 제공한다는 점에서도 무척 유익하지만, 무엇보다 그것이 내 일상과 어떤 부분에서 접접을 가지는지를 체감하고 흥미를 가질 수 있도록 만든다는 점에서 추천하고 싶다. 단락들을 읽어나가며 추가로 읽어보고 싶은 도서들로 확장 연결되는 부분들도 또 하나의 재미다. 어렵게 느껴질 수 있는 부분들을 쉽고 재미있게, 직관적으로 설명해낼 수 있는 힘이 있는 저자라 읽는 동안 즐거웠다.
다만, 지구에서 가장 가까운 블랙홀의 경우는 확인이 필요하다. OGLE-2011-BLG-0462(Sagittarius)은 기존의 A0620-00(Monoceros)보다도 멀어서, 궁수자리의 블랙홀이 지구에서 가장 가깝다는 부분은 수정이 필요한 것 같다. 무엇보다 22년 11월 새로운 블랙홀로 1560광년 거리의 뱀주인자리 블랙홀 Gaia BH1(Ophiuchus)이 발견되었으므로 어쨌거나 상황이 바뀌었다.
그리고 약간의 욕심을 더한다면 블랙홀과 입자/반입자 부분에 추가 설명이 들어가면 좋겠다. 블랙홀의 경계 - 사건의 지평선에서 입자가 외부에 남을 수도 있지만 반입자가 외부에 남을 수도 있기 때문이다. 기본적으로 경우의 수는 반반이다. 그럼에도 입자-물질이 조금 더 다수가 되어 현재의 우주가 되었다는 점과, 블랙홀의 내부로 남겨지는 것은 어느 쪽이든 음에너지를 가지는 쪽이라는 점에 대해 다뤄지면 더 좋지 않았을까 싶지만, 이건 개인적인 욕심이다.
그 외에도 아인슈타인이나 푸앵카레 등의 일화에서 한 방면에서 뛰어난 이들이라고 해도 새로운 것을 받아들이는 것에는 얼마나 완고할 수 있는지, 도형의 중첩으로 4차원을 나타내는 차원기하학과 중세의 신성기하학 간의 유사성 등 흥미로운 포인트가 많았다. 지구는 둥글지만 원은 아니라는 점에서, 완전히 옳은 것도 완전히 틀린 것도 없을지도 모른다. 현재까지 변하지 않는 진리는 '광속' 뿐이다.
즐겁게 읽었다.
고대 그리스의 철학자
헤라클레이토스 Heraclitus는 이런 말을 남겼다.
"우리는 똑같은 강물 속에 두 번 들어갈 수 없다.
다른 강물들이 계속 들어오기 때문이다."
우리는 하루하루 도대체 왜 살아갈까? 누군가 묻는다면, 갑자기 우리 머릿속은 하얗게 바뀌며 반사적으로 사고를 멈춘다. 사는 곳이 어디인지 혹은 취미가 무엇인지 정도의 가벼운 질문이라면, 보통 몇 초 만에 답할 수 있다. 하지만 이런 유형의 질문은 평소에 충분히 대비되어 있지 않아 뭐라고 대답하기가 어렵다. 답하기 어려운 질문이란 어쩌면 굉장히 좋은 질문이며, 지금 우리에게 무언가 도전할 기회를 줄지도 모른다.
- 빅뱅 직후의 우주를 관측하기 위해 인류 최고의 새 우주망원경을 지구로부터 150만 킬로미터 떨어진 곳에 올리기도 한다. 이런 과학기술들이 놀랍긴 하지만, 지금의 우리와 크게 관련이 없는 것도 사실이다. 그런데 이런 연구가 우리에게 왜 필요할까? 결과가 눈앞에 드러나지 않는다면, 과연 정말 중요한 문제인 걸까? 그렇지 않다면 어떤 게 중요할까? 중요하다는 건 무슨 뜻일까? 오늘만 살아가는 우리가 무엇이 중요한지 제대로 구분할 수 있기나 할까?
- 만약 인류가 처한 상황이 이와 유사하다면 어떨까? 보유하고 있는 가치 대부분을 오직 현재라는 시점에 판돈으로 걸고 있지만, 사실 이 모든 건 어느 순간 엉망이 되어버린 노름판처럼 무의미해질지도 모른다. 지구온난화로 지구의 평균기온이 섭씨 2도만 올라가도 절반 이상의 생물종이 멸종할 것이다. 소행성이 충돌하거나 슈퍼 화산이 폭발한다면, 우리의 보금자리조차 더는 생명체가 살아갈 수 없는 환경이 될 것이다. 이게 내 통장 잔액을 건드리는 것만큼 무서운 일은 아닐지라도, 결코 시시한 일로 치부해 버려서는 안 된다. 인류의 생존과 직결된 이런 상황을 두고도 별다른 감흥이 없다면, 가족과 친구, 사랑하는 모든 이가 앞으로 경험할 혹독한 환경과 어렵게 끌고 나갈 생의 마지막 숨결에도 아무런 관심이 없다는 뜻과 같다.
- 다행히 컴퓨터가 선택할 모든 미래는 결정되어 있는데, 당연하게도 선택지 자체가 전부 프로그램 코드로 쓰였기 때문이다. 자동판매기에 동전을 어떤 방식으로 넣어도 나올 수 있는 음료수가 정해져 있는 것과 마찬가지다. 미래가 이미 정해져 있다면, 사실상 아직 오지 않은 '다음'이라는 말은 의미가 없고 모든 미래는 그저 상태일 뿐이다. 영화를 보다가 재생 바를 움직이면 원하는 장면에 도달할 수 있는 것처럼, 컴퓨터로 만들어진 세상에서는 시간대를 자유롭게 이동할 수 있을지도 모른다.
- 예측할 수 없다는 것과 결정되어 있지 않다는 건 어찌 보면 비슷해 보이지만, 완전히 다르다.
- 상상력 혹은 창의성은 기존에 없던 생각이나 개념을 찾아내는 과정으로 인간 고유의 능력이라고 한결같이 여겨져 왔기 때문에, 과학자들은 인간의 뇌 어딘가에 이것만을 관장하는 영역이 있으리라고 확신했다. 하지만 어처구니없게도 그 영역은 기억이 저장되는 곳과 동일했다. 모방이 창조의 어머니라던 고대 그리스의 철학자 아리스토텔레스 Aristoteles의 말처럼, 새로운 것도 결국 기존의 저장된 기억들로부터 나온 것일 뿐이었다. 창의성은 기억에서 온다. 이 논문은 국제 학술지 <사이언스 Science>의 세계 10대 과학 성과로 선정되었고, 훗날 수십만 장의 기보를 집어넣은 알파고는 저장된 데이터를 바탕으로 매우 창의적인 수를 두게 되었다.
- 홍콩의 영화배우 주성치가 출연한 명작 중에 <서유기 Journey to the West>라는 작품이 있다. 극 중 주성치의 대사에 이런 부분이 있다. "진정한 사랑이 눈앞에 나타났을 때, 나는 이를 소중히 여기지 않았지. 만약 하늘에서 다시 기회를 준다면, 사랑한다 말하겠소. 기한을 정하라고 한다면, 1만 년으로 하겠소." 사랑의 기한을 무려 1만 년으로 설정하면서, 진심을 담은 고백을 전하는 상황이다. 하지만 양자컴퓨터가 등장하면서 1만 년의 시간이 우스워지고 있다. 당대 내로라하는 슈퍼컴퓨터가 최소 1만 년 이상 걸리는 계산을 단 200초 만에 풀어냈기 때문이다.
(리뷰자 주 : 아니, <서유기>라고만 표기하면 어떻게 합니까!!! 선리기연과 월광보합을, 자하선사를 그렇게 흘려 넘겨 버리다니!)
- 더 빨라질 수 있는 다른 방법은 없을까? 이걸 고민하다가, 근본적인 질문으로 돌아갔던 과학자가 있었다. 바로 영국의 이론물리학자 데이비드 도이치 David Deutsch였다. 그는 생각했다. '우리는 지금 과연 컴퓨터를 제대로 만들고 있는 걸까? 지금의 컴퓨터는 0과 1로 계산하고 있지만, 양자역학적으로 보면 정보의 상태는 0과 1, 오직 두 가지만 존재하는 것이 아니다. 0이면서도 동시에 1인 중첩 상태 superposition도 고려해야 하지 않을까?' 이렇게 양자컴퓨터의 기본 단위인 큐비트 qubit, quantumbit가 탄생했다. 양자역학적으로 정보는 관측하기 전까지 0이면서도 1인 중첩 상태를 갖는다. 정보의 중첩이 도대체 속도와 무슨 관계가 있을까?
- 기회는 평등하고 과정은 공정하며 결과는 정의로운 것이 정말 있다면, 바로 시간일 것이다.
- 그런데 정말 그럴까? 시간이 흐르는 속도가 동일한지를 확인하기 전에, 먼저 시간이 무엇인지를 알아보자.
(리뷰자 주 : 카를로 로벨리의 <시간은 흐르지 않는다>를 읽어보시길 추천한다.)
- 마땅히 좋은 표본을 구하기가 어려워 연구가 늘 난항이던 어느 날, 좋은 기회가 찾아왔다. 미국 미네소타주에 있는 수녀원에서 의학 발전을 위해 자발적으로 뇌를 기증하기로 한 것이다. 100세가 넘도록 장수한 수녀가 무려 7명이나 되고, 수녀 대부분이 치매 증상 없이 건강하게 오래 살았기 때문에 사후 기증받은 뇌를 통해 알츠하이머병 예방에 대한 많은 단서를 얻을 수 있을 거라고 믿었다.
- 기대처럼 건강한 두뇌를 갖고 있지는 않았지만, 이미 심각한 알츠하이머병이면서도 그 증상이 발현되지 않았던 특별한 경우들을 발견한 것이다. 도대체 어떻게 이런 일이 가능할까? 뇌에는 기억이 저장되는 시냅스라는 부분이 있는데, 뇌세포들의 의사소통을 위해 연결된 길이라고 생각하면 좋다. 시냅스가 복잡하게 연결될수록 기억이 단단하게 남아 있는 것으로 볼 수 있는데, 수녀들의 시냅스는 정말 무시무시하게 복잡한 연결을 형성하고 있었다. 그녀들은 끊임없이 공부하고 생각하며 뇌를 관리해 왔다. 기억을 하나의 시냅스에만 저장하지 않고 새로운 시냅스를 계속 연결해 가며, 알츠하이머병으로 일부 연결이 끊어져도 나머지 시냅스로 마치 벤치의 후보 선수들처럼 뛰쳐나가 그 자리를 채워준 것이다.
- 지난 수십 년 동안 꿈꾸는 행위는 주로 렘수면 단계에서 대부분 일어난다고 알려져 있었다. 아쉽게도 나이가 들수록 전체 수면 시간 중에서 렘수면이 차지하는 비중이 줄어드는 경우가 많아서 어릴 때보다 꿈꾸는 횟수가 줄어든다는 말도 있다. 하지만 최근 연구에 따르면, 비렘수면 단계에서도 꿈꿀 때 발생하는 신호가 포착되는 정황이 나타났다. 렘수면 단계에서만 꿈을 꾸는 게 아닐 수도 있다는 말이다. 상반되는 여러 주장이 계속 나오는 상황에서, 2017년에 미국 위스콘신대학교의 신경과학자들은 렘수면과 비렘수면 단계 모두에서 꿈을 꿀 수도 있고 꾸지 않을 수도 있다고 밝혔다. 단순히 어떤 수면 단계에서 꿈을 꾸는 것이 아니라 뇌의 후두부에 있는 '핫 존 hot zone'이 활성화되면 꿈을 꾼다는 주장이었다.
- 우리가 살면서 보고 듣고 느끼는 모든 감각 정보는 전기신호로 변경되어 뇌로 들어오고, 같은 경험을 할 때마다 전달되는 동일한 패턴의 신호는 흔적으로 남게 된다. 그리고 우리는 이걸 '기억'이라고 부른다. 예를 들어, 사과를 보면 뇌에서는 사과에 대응하는 신호 패턴이 발생하는데, 특정한 신호 패턴이 계속 오고 가기를 반복하면 우리는 사과의 모습을 명확하게 기억하게 되고 이로써 점차 발전된 지능을 갖추게 된다. 그런데 이러한 신호 패턴이 뉴런들 사이를 오갈 때마다, 이 신호로 인해 일종의 전기적인 파동도 함께 발생한다. 머리뼈의 안쪽에는 뇌가 경뇌막, 거미막, 연뇌막이라는 세 겹의 막으로 싸여 있다. 더 깊이 들어가면 대뇌피질에서 시냅스가 신경전달물질을 분비하는데, 좀 더 자세히 들여다보면 신경세포 외부에 있던 나트륨 이온이 세포 안으로 유입되고 칼륨 이온은 반대로 세포 밖으로 나가면서, 세포막 사이에 전위차가 발생한다.
(리뷰자 주 : 동일 전위인 두 이온의 교환이 어째서 전위차를 발생시킬까? 여기서는 우선 채널과 펌프라는 수동과 능동 이동의 개념이 필요하다. 세포막에는 에너지를 소모하는 펌프와 그렇지 않은 채널이라는 통로가 존재한다. 안정기의 세포는 기본적으로 'Na+ 채널'보다 수가 많은 'K+ 채널'로 인해 세포 안은 칼륨, 세포 밖은 나트륨의 농도가 높으며 그 외 단백질과 이온 분포로 인해 음전위(-70mV)를 띠고 있다. 하지만 자극을 받아 (전압자극) Na+채널이 열리게 되면서 농도적 기울기에 의해 Na+는 안으로 이동하며 전위가 상승하게 되고(탈분극, 활동전위 발생), 이후 K+채널이 열리면 K+는 밖으로 이동하며 다시 분극 상태로 돌아오게 된다. 이 과정에서 에너지를 소모해 3개의 Na+와 2개의 K+ 이온을 맞교환하는 Na+/K+ 펌프가 중요한 역할을 하게 된다.)

- 전기장으로 인해 자기장이 생성되고 자기장의 변화가 다시 전기장을 생성하다 보면 파동이 발생한다. 사실 각각의 뉴런에서 발생하는 파동은 매우 미약하다. 하지만 셀 수 없이 많은 뉴런들에서 파동이 복합적으로 발생하면, 우리가 측정할 수 있을 만한 크기의 파동이 모습을 드러낸다. 이게 바로 뇌파의 정체다.
- 기본적으로 다섯 가지 뇌파가 잘 알려져 있다. 이들은 보통 주파수로 구분되는데, 가장 낮은 주파수인 델타파부터 시작해, 세타파, 알파파, 베타파, 감마파가 있다. 보통 델타파는 깊은 수면 상태에 나오며, 세타파는 수면과 깨어 있는 상태의 중간 정도에서 나온다. 무언가에 집중하지 않은 상태로 눈을 감고 편하게 있으면 알파파가 나오며, 눈을 뜨고 집중하는 상태에서는 베타파가 주를 이룬다. 가장 높은 주파수인 감마파의 경우, 고도의 인지 정보를 처리하거나 초조한 상태에서 나오는 것으로 알려져 있다. 뇌파를 통해 우리가 어떤 상태인지를 알아낼 수 있다는 사실은 매우 흥미로운 결과였고, 반대로 뇌파를 바꿔서 뇌의 활동에 영향을 미칠 수는 없을까 하는 아이디어도 등장하기 시작했다. 그중에서도 소리는 가장 안전하고 손쉽게 사용할 수 있는 도구였다.
- 자세한 내용을 알기 전까지 뇌파는 정말 신비로운 대상이었지만, 잘 들여다보면 사고하는 생명체에서 당연히 발생할 수 있는 전기적 신호다. 우리 몸의 수많은 복잡한 동작 역시, 신경 활동에 의해 발생하는 뇌의 미세한 전기신호가 온몸에 퍼져 있는 근육에 영향을 미치기 때문에 가능하다. 우리 몸은 전기로 가동되는, 생명공학 기반의 생체 로봇인 셈이다. 따라서 뇌가 일할 때마다 뇌파가 발생하며, 뇌파를 측정한다는 것은 뇌 활동을 측정한다는 의미다. 뇌파를 통해 잠을 자고 있는지 아니면 깨어 있는지를 확인할 수 있고, 뇌의 기능에 이상이 있는지도 알 수 있다. 가까운 미래에는 겉으로 드러나는 대화 없이 상대가 원하는 바를 바로 읽어내고, 나아가 서로 뇌파만으로 대화를 나눌 수 있는 시대가 도래할지도 모른다. 하지만 아직 우리가 뇌파를 통해 타인의 감정과 생각을 읽어내거나 숨겨진 의도를 파악하는 건 쉽지 않다.
- 우리 은하 중심에는 아주 거대한 블랙홀이 존재한다. 블랙홀을 질량으로 구분하면 두 가지로 나눌 수 있다. 바로 항성질량 블랙홀 stellar-mass black hole과 거대질량 블랙홀 supermassive black hole이다. 전자는 태양보다 수십 배가량 무겁고, 후자는 수십만 배에서 수십억 배 더 무겁다. 우리 은하 중심, 궁수자리A 근처에 있는 블랙홀은 거대질량 블랙홀이면서 지구에서 가장 가깝다. 또 연구할 만한 녀석은 처녀자리 은하단의 M87 은하 중심에 있는 거대질량 블랙홀이다. 굉장히 멀리 있긴 하지만, 그만큼 커서 지구에서 보이는 크기는 둘이 비슷하다. 2008년과 2012년에 각각 두 블랙홀의 사건의 지평선 크기를 여러 망원경의 간섭계를 통해 측정했지만, 분해능이 낮아 제대로 관측했다고 보기는 어려웠다. 둘 중 먼저 볼 녀석을 골라서 제대로 봐야 했다.
(리뷰자 주 : 궁수자리A 근처의 블랙홀은 OGLE-2011-BLG-0462를 말하는 것 같은데, 이 블랙홀은 약 5000광년 거리로 1986년 블랙홀로 확인된 3000-4700광년 거리의 외뿔소자리 블랙홀 A0620-00보다 멀다. 지구에서 가장 가까운 블랙홀은 A0620-00이었다. 다만 현재는 며칠 전 관측된 지구로부터 약 1560광년 거리에 위치한 뱀주인자리 블랙홀 Gaia BH1이 항성질량 블랙홀이자 가장 지구에서 가까운 블랙홀이 되었다.)

- 우리는 더 멀리 볼수록 과거를 보며, 파장이 긴 적외선으로는 훨씬 더 멀리까지 볼 수 있다. 그래서 제임스 웹 우주망원경은 허블 우주망원경보다 더 먼 과거를 볼 수 있고, 최초의 별이나 은하를 연구할 수도 있으며 이들이 어떻게 형성되고 죽어가는지, 그리고 외계 생명체 탐사나 생명의 기원도 연구할 수 있다. 수많은 과학자의 기대와 염원을 한 몸으로 받아낸 제임스 웹 우주망원경은 아주 희미한 천체들도 빠뜨리지 않고 꼼꼼하게 담아낼 텐데, 이제 공식적인 첫 번째 사진이 공개될 차례가 다가오고 있었다.
- 죽어가는 별의 모습을 포착한 세 번째 사진, 여러 은하가 모여서 연주를 하는 네 번째 사진 그리고 별이 탄생하는 마지막 사진도 순차적으로 공개되었다. 남쪽 고리성운 Southern Ring Nebula은 태양 정도의 질량을 가진 별이 죽어가며 흔적을 남긴 행성상 성운인데, 진화의 마지막 단계에서 거대한 가스가 얼마나 아름답게 뿜어져 나왔는지를 상세히 확인할 수 있었다.
- 한 가지 예로, 참신한 아이디어로 종교재판까지 받으면서도 지구가 돈다고 믿었던 갈릴레오의 고민이 있었다. 지구가 빠르게 돌고 있다면, 왜 우리는 지구가 도는 걸 느끼지 못할까? 혹시 우리도 지구 위에 올라타서 함께 운동하고 있기 때문은 아닐까? 마치 빠르게 항해하는 배 위에서 떨어뜨린 동전이 갑판 위로 그대로 떨어지는 것처럼 말이다. 당시 갈릴레오는 놀랍게도 모든 운동이 상대적이라는 것을 알아냈다. 동전은 배에 대해서, 배는 동전에 대해서 각각 서로를 바라보며 움직이기 때문에, 배 위에서 동전을 떨어뜨리는 것만으로는 배가 정지해 있는지 움직이는지 알 수 없다는 것이다. 이처럼 정지한 상태와 운동하는 상태의 구별은 불가능하다.
- 당시 사람들은 세상 모든 만물이 흙, 불, 공기, 물, 이렇게 네 가지 원소로만 이루어져 있다고 믿었다. 그리고 여기에 빛의 매질을 추가하게 된다. 바로 다섯 번째 원소인 에테르의 등장이었다. 에테르는 우주 전체에 균일하게 퍼져 있으며, 맥스웰 방정식은 에테르가 고요하게 정지해 있는 공간에서 정확하게 들어맞는다고 생각되었다. 물론 실험적으로 검증된 적은 없었지만 말이다.
- 하나의 절대적인 가정을 완벽하게 지켜내기 위해 그것을 제외한 모든 것을 지극히 상대적으로 바꿔버리는 이론이라는 것이다. 그 절대적인 가정은 바로 빛의 속력! 누가 어디서 관측하든, 빛은 늘 일정한 속력을 갖는다. 그리고 이를 유지하기 위해 시간과 공간이 상대적으로 바뀌는 것이 바로 상대성이론이다.
- 1908년 독일의 수학자 헤르만 민코프스키 Hermann Minkowski는 과학자 모임에서 이런 연설을 남겼다. "앞으로 시간과 공간은 마치 그림자처럼 사라질 것이며, 오직 그 둘이 합쳐진 시공간만이 독립적인 실체로 남을 것이다." 특수 상대성이론을 쉽게 표현하는 기하학적 방법인 민코프스키 시공간의 탄생이었다. 이제 우리는 모두 시간과 공간이 서로 분리되어 있지 않다는 것을 알고 있다. 또한, 아인슈타인의 유명한 식인 질량과 에너지의 관계도 여기서 나왔다. 고전역학에서는 정지한 물체가 에너지가 있다는 건 말도 안 되는 이야기였지만, 특수 상대성이론에 따르면 정지해 있어도 질량만 있다면 에너지를 갖는다.
- 빛의 속력은 우주가 정한 자연법칙의 최고 속력이라고 볼 수 있다. 게다가 빛의 속력은 어마어마하게 빠르니, 일상생활 속 느려 터진 사건들은 고전역학으로도 충분히 설명된다. 프랑스의 철학자 오귀스트 콩트 Auguste Comte는 이런 말을 남겼다. "모든 것은 상대적이다. 오직 이 사실만이 절대적이다." 과연 그럴까? 아니다. 오직 빛의 속도만이 절대적이다.
- 일반적인 설명은 여기까지지만, 실제로는 이렇게 간단하지 않다. 상식선에서 이해하는 무질서도만으로 엔트로피를 설명하는 건 불완전하기 때문이다. 컵이 깨져 있건 잘 붙어 있건 컵을 구성하는 입자의 관점에서는 확률적으로 큰 차이가 없다. 물질을 구성하는 배열만 봐서는 무엇이 더 무질서한 지를 구분할 수 없다는 말이다. 오히려 물질이 놓여 있는 공간의 크기를 고려하는 것이 중요하다. 컵이 놓여 있는 식탁 위의 공간 전체를 생각해 보자. 컵을 구성하는 아주 작은 부스러기들이 식탁 한편에 모여 컵을 이루고 있거나 부서진 채로 식탁 전체에 퍼져 있을 경우의 수를 각각 계산해 보면, 부서져 있는 경우가 비교할 수 없을 만큼 훨씬 많을 것이다. 그래서 부서진 컵 조각들이 자연스레 깨지지 않은 컵으로 돌아가는 경우는 거의 없지만, 컵이 깨져서 조각나는 경우는 쉽게 발생한다.
(리뷰자 주 : 이는 중첩과 멀티버스와도 연결되는 내용이다.)
- 주어진 공간 안에서 가능한 경우의 수가 작다면 엔트로피가 낮다고 표현하며, 반대일 경우 엔트로피가 크다고 한다. 현실 세계는 식탁 위보다 끝없이 넓고 컵의 부스러기들보다 갖가지 다양함이 가득하기에, 자연에서 존재하는 모든 변화는 반드시 엔트로피가 증가하는 방향으로 일어난다. 특히 우주 역시 물질과 에너지의 출입이 없이 고립된 거대한 공간이라고 볼 수 있기에, 우주 전체의 엔트로피는 늘 증가한다.
(리뷰자 주 : 이 가정과 시간이 1차원이라는 가정이 현재의 차원을 규정하는 대전제라고 생각한다. 이것은 주춧돌이 될 수도, 천장이 될 수도 있다.)
- 이건 과연 무슨 의미일까? 항상 움직이며 한쪽으로 향하는 기준이 있다면, 우리는 이것을 '우주적 흐름'이라고 부를 수 있다. 바로 시간이다. 우주에 존재하는 모든 물질과 에너지 역시 언젠가 우주 전체에 고르게 퍼질 것이며, 가장 높은 확률을 갖는 형태에 도달하고 나면 더는 변하지 않는 채로 멈출 것이다. 우주 종말을 설명할 수 있는 하나의 개념이 있다면 아마도 엔트로피 일지도 모른다.
- 하지만 물리학자들이 말하는 정보는 좀 다르다. 그들에게 정보란 모든 입자의 양자적 특성인 '양자 정보'가 보다 익숙하다. 책의 정보는 제목이나 내용이 아닌, 책을 구성하는 입자들이 어디에 어떤 구조로 모여 있는지, 얼마나 빠른지, 어떻게 도는지와 같은 양자 정보를 의미한다. 우주에 존재하는 모든 물질은 이러한 양자 정보를 갖는 입자들로부터 만들어진다.
(리뷰자 주 : 최근 그림을 그리고 있어서 그런지 일종의 코드값처럼 느껴지기도 한다. 하나의 픽셀은 모든 정보를 가질 가능성이 있지만 하나의 값만을 가지며 결과적으로 프로그램 내에 존재한다. 그림을 그리는 동안 감각되는 색의 중첩은 실제로는 단일한 픽셀 값의 변화일 뿐이다.)
- 정보를 연구하는 과학자들은 현대 물리학의 기반이 되는 매우 중요한 두 가지 법칙을 만들었다. 정보는 어떠한 경우에도 파괴되지 않으며, 우주에 존재하는 모든 정보의 총량은 반드시 보존된다는 것이다. 책이 불에 타서 잿더미가 되더라도, 원래 정보는 그대로 남아 있어야 한다. 책에 가해진 에너지를 꼼꼼히 계산하고 입자를 하나하나 모아 재구성하는 게 가능하다면, 책을 다시 원래대로 만들어 낼 수 있다. 정보는 절대 파괴되지 않고, 사라지지 않기 때문이다. 원래 책의 정보가 굉장히 해석하기 어려운 정보로 형태가 바뀐 것뿐이다. 이게 무너지면, 인류가 지금까지 쌓아 올린 모든 과학적 발견은 전부 새롭게 바뀌어야 한다.
- 그런데 문제가 생겼다. 일어나서는 안 되는 그 일이 벌어진 것이다. 블랙홀이라는 강력한 천체의 발견은 과학자들에게 공포를 선사했다. 빛까지 빨아들이는 무시무시한 중력 때문이 아니다. 정보와 관련된 절대적인 법칙을 블랙홀이 무너뜨려 버리기 때문이다. 블랙홀은 막대한 질량이 아주 작은 한 점에 집중되어 있을 때 만들어진다. 물론 차원조차 의미가 없기에, 실제로는 점도 아니다. 사건의 지평선이라는 경계를 넘으면, 블랙홀과 블랙홀을 제외한 모든 건 철저히 분리된다.
- 호킹 복사는 이론상으로만 존재하는 양자 중력의 현상 가운데 하나로, 블랙홀이 방출하는 열 복사선을 의미한다. 사실 텅 비어 있는 것처럼 보이는 진공상태를 아주 작은 세계에서 바라보면, 입자와 반입자가 무한히 생성되었다가 서로 충돌하며 소멸하기를 반복하고 있다. 이런 현상은 우주의 모든 곳에서 일어나고 있는데, 막상 우리는 불확정성 원리 uncertainty principle로 인해 이를 볼 수 없다. 너무 짧은 시간 동안 나타났다 사라지기 때문이다. 호킹은 이 현상이 일어나는 장소를 블랙홀 근처로 옮기는 참신한 아이디어를 떠올려, 우주에 존재하는 가장 거대한 천체와 아주 작은 양자 세계의 현상을 연결했다. 정확히 말해, 사건의 지평선을 사이에 두고 생성된 입자와 반입자는 바로 다시 만나서 사라지려고 하지만, 사건의 지평선 때문에 둘은 완벽히 분리되어 버린다. 블랙홀 안쪽의 반입자는 결국 내부의 입자를 만나 사라질 테고, 바깥쪽의 홀로 남은 입자는 반입자를 찾아 떠난다. 결과적으로 블랙홀 안에는 입자가 하나 줄고, 블랙홀 밖의 세상에는 입자가 늘어난다. 1974년에 호킹은 블랙홀들이 아주 오랜 시간에 걸쳐 이러한 호킹 복사를 통해 사건의 지평선에서 입자를 조금씩 내보낼 수 있다고 주장했다.
(리뷰자 주 : 조금 더 정확하게는, 블랙홀은 음의 에너지를 가지는 쪽을 흡수한다. 반드시 반입자를 선택해서 흡수하는 것은 아닌데, 아주 약간 균형이 틀어져 입자의 세계인 현재의 물질 우주가 탄생했다. 사실 반물질의 우주라고 불러도 상관없다. 물질이든 반물질이든 '많은 쪽'이 그 우주의 '물질'이 되기 때문이다.)
- 요즘에는 종이책 대신 전자책도 많이 읽는다. 둘은 기록하는 방식이 완전히 다르지만, 똑같은 내용이 들어가 있다. 즉, 블랙홀은 3차원에 있는 정보를 2차원에 암호화해 기록하는 존재라는 뜻이다. 이처럼 평면상에 입체를 기록하는 기술이 있는데, 바로 홀로그램이다. 만약 3차원의 정보가 사건의 지평선에 2차원 형태로 저장된다면, 호킹 복사를 통해 암호화된 정보를 옮기는 것도 가능하다. 다시 말하면, 정보는 블랙홀과 무관하게 파괴되지 않으며, 이로써 현대 물리학도 무너지지 않게 되는 것이다. 이것이야말로 정보 역설을 해결하는 유일한 방법이다. 여기서 한 단계만 더 나아가 보자. 만약 우주가 홀로그램이라면, 그곳에 빨려 들어간 사람은 어떻게 될까? 아마 평소와 다름없는 세계를 경험할 것이다. 바깥에서 보면 2차원의 평평한 모습이겠지만, 같은 차원인 내부에서는 어색하지 않을 가능성이 크다. 그런데 우리 자신이 비슷한 처지에 있다면 어떨까? 이미 블랙홀 표면에 2차원으로 암호화되어 있는데 그 사실을 느끼지 못할 뿐이라면, 현실이 정말 3차원이라는 것을 증명할 수 있을까?
- 관측 가능한 우주라는 개념이 있다. 빛의 속도보다 빠르게 멀어지는 영역은 관측할 수 없으며, 인류가 볼 수 있는 우주의 한계가 정해져 있다는 뜻이다. 혹시 이것이 3차원인 우리 우주를 둘러싼 2차원의 표면으로 이루어진 경계는 아닐까? 마치 블랙홀 사건의 지평선처럼 말이다. 만약이게 사실이라면, 우리의 현실은 단지 그 정보를 홀로그램처럼 투영한 것이며, 실체는 여기 대신 우주의 바깥에 존재할지도 모른다. 인류에게 흥미로운 숙제를 남긴 스티븐 호킹은 이렇게 말했다. "신이 주사위를 던지지 않는다고 말한 아인슈타인은 틀렸다. 블랙홀을 떠올리면, 신은 아마 주사위를 우리가 볼 수 없는 곳에 던져놓을 것이다." 언젠가 인류가 블랙홀의 비밀을 풀고 신이 던진 주사위라는 진리에 다가가는 날을 기대해 본다.
- 물리학에도 비슷한 사례가 있다. 바로 끈 이론이다. 사실, 끈 이론 혹은 초끈 이론 super-string theory에 대해 과학자 대부분은 회의적인 관점을 갖고 있다. 미국의 천재 물리학자 리처드 파인먼 Richard Feynman은 아무것도 알아낼 수 없는 초끈 이론을 완전히 엉터리라고 부르며, 끈 이론의 창시자 중 한 명인 존 슈워츠 John Schwarz를 만날 때마다 오늘은 몇 차원에 계시냐고 놀렸다. 약력과 전자기력의 통합 이론에 대한 공로로 노벨 물리학상을 수상한 셸던 글래쇼 Sheldon Glashow도 끈 이론을 연구하는 학자들이 학생들을 타락시키고 있으며, 그들의 연구는 물리학이 될 수 없다고 말했다. 심지어 네덜란드의 물리학자 헤라르뒤스 엇호프트 Gerardus 't Hooft는 끈 이론이 이론이나 모형이 아니라 직감일 뿐이라고 주장했다. 끈 이론이 이렇게 혹독하게 비판을 받으면서도 아직까지도 연구되는 이유가 단지 아름답기 때문이라면 믿을 수 있겠는가? 수학적으로 매우 아름답기에 그것으로 충분하며, 증명할 필요조차 없다고 주장하는 학자들이 있는데, 여기서 '아름답다'는 말은 도대체 무슨 뜻일까?
(리뷰자 주 : 놀랍게도(?) 대부분의 연구는 하나의 가설을 긍정하는 연구와 부정하는 연구 모두 동시에 존재한다. 그것이 '정설'이 되는 것은 각각의 존재 비율의 문제일 뿐이다. 이상하지 않은가? 양쪽을 주장하는 이들은 모두 '과학자'들인데 말이다. 현대 과학은 하나의 가설이 '정설'로 받아들여지면 '합리적인' 과학자들은 모두 그것을 받아들여 새로운 계단 위로 올라간다고 가정하지만, 사실 반드시 그런 것만은 아니다. 또한 기본적으로 과학은 그 계 안에서 발생하는 '현상'을 통해서 해당 계에서 작동하는 규칙을 찾아내는 학문이다. 따라서 한 가설이 '정설'이 되기 위해서 조건 지어지는 제한 사항들 하에 그것은 '재현 가능성'이 높은 '법칙'이 되는 것이며, 대개 계를 달리하면 힘을 잃는 경우가 많다. '어떤 기준점'에서 보느냐에 따라 달라지기도 한다는 점, 확고한 진리는 없었다는 점, 과연 우리는 과거의 발견들을 토대로 '앞으로' 나아가고 있는 것인가 하는 점들을 고려해볼 때 일부 과학도들이 가지는 재단적인 시야는 다소 편협하지 않은가 생각한다. 이미 파훼된 규칙을 믿고 있는 것과 증명되지 않은 현상을 믿고 있는 것 사이의 차이가 모호하다면, 어느 한쪽이 미신이라고 불려야 하는가는 개인의 성향에 달린 문제가 될 것이다.)
- 신의 존재를 과학적으로 검증할 수 없는 이유는, 반증할 방법이 없기 때문이다. 과학적인 검증을 하기 위해서는 반드시 반증 가능해야 한다. 도무지 믿기 힘들었던 양자역학 역시, 양자역학의 확률론적 해석을 반증할 수 있는 아이디어가 나오고 실험을 통해 이런 반증 아이디어가 틀렸다는 게 확인되면서 과학 이론으로 정립된 것이다. 하지만 끈 이론은 지금으로서는 입증도 반증도 할 만한 어떠한 실험적 방법론도 생각할 수 없다는 게 큰 문제다. 수학적으로는 깔끔하게 네 가지의 기본 힘을 통합할 수 있는 유일한 이론이지만, 아주 작은 끈의 형태가 11차원에 존재한다는 전제부터 검증할 방법이 없다. 누구도 여분의 차원을 관측하거나 관측할 방법을 찾을 수 없다. 이걸 과연 과학 이론이라고 볼 수 있을까?
- 아인슈타인은 이렇게 말했다. "삶을 사는 데는 두 가지 방법이 있다. 하나는 기적이 전혀 없다고 여기는 것이고, 다른 하나는 모든 것이 기적이라고 여기는 것이다." 모든 법칙을 통일하지 못했다고 의미 없다고만 할 수 없다. 초끈이론을 포함해 지금까지의 모든 과정은 전부 기적이었다.
- 과거에는 3차원부터 내려오는 형태로 차원을 상상했기에, 유클리드는 입체의 끝은 면, 면의 끝은 선, 선의 끝은 점이라는 표현을 썼다. 아쉽게도 그리스의 철학자 아리스토텔레스 역시 3차원 이상의 차원이 없다고 말했지만, 프랑스의 수학자 앙리 푸앵카레의 생각은 달랐다. 차원을 기존과 반대로 정의한 그는 끝이 0차원 점이 되는 것이 1차원이라고 말했다. 그렇다면 끝이 1차원 선이라면 2차원, 끝이 2차원 면이라면 3차원이 되는 것이다. 이렇게 올라가면, 끝이 3차원 입체인 4차원이라는 새로운 차원을 생각할 수 있다. 입체가 차원의 꼭대기가 아니라 더 높은 차원까지 계속 이런 방식으로 얼마든지 올라갈 수 있게 되는 것이다.
- 점을 움직이면 선, 선을 움직이면 면, 면을 움직이면 입체, 그렇다면 입체를 움직이면 입체의 다음 단계인 초입체가 등장한다. 다시 말해, 선은 2개의 점으로 둘러싸여 있으며, 면은 4개의 선, 입체는 6개의 면으로 둘러싸여 있다. 그렇다면 간단하다. 초정육면체 역시 8개의 정육면체로 둘러싸여 있으면 된다. 물론 4차원 공간에서만 가능한 형태라서 현실에 존재하는 어떠한 입체도형도 8개의 정육면체로 둘러싸일 수는 없다. 초정육면체가 아닌 다른 4차원 형태는 더 복잡해지긴 하지만, 중요한 건 차원을 기하학적으로 접근할 수 있다는 사실이다.
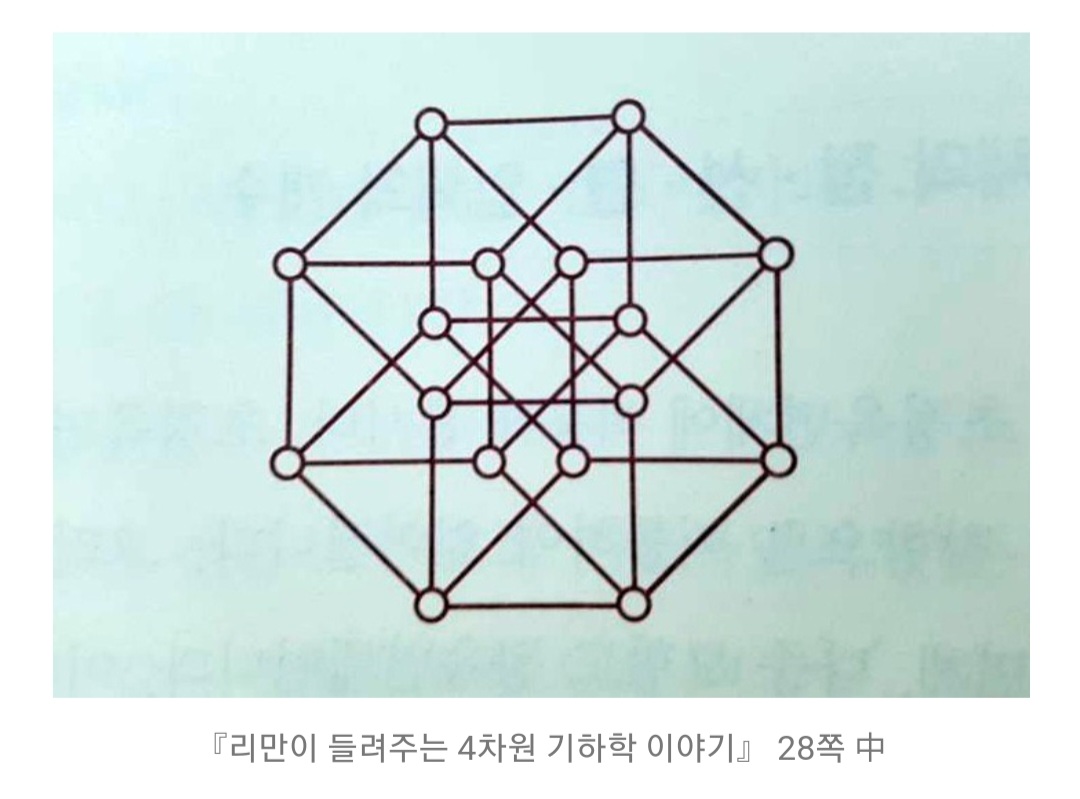
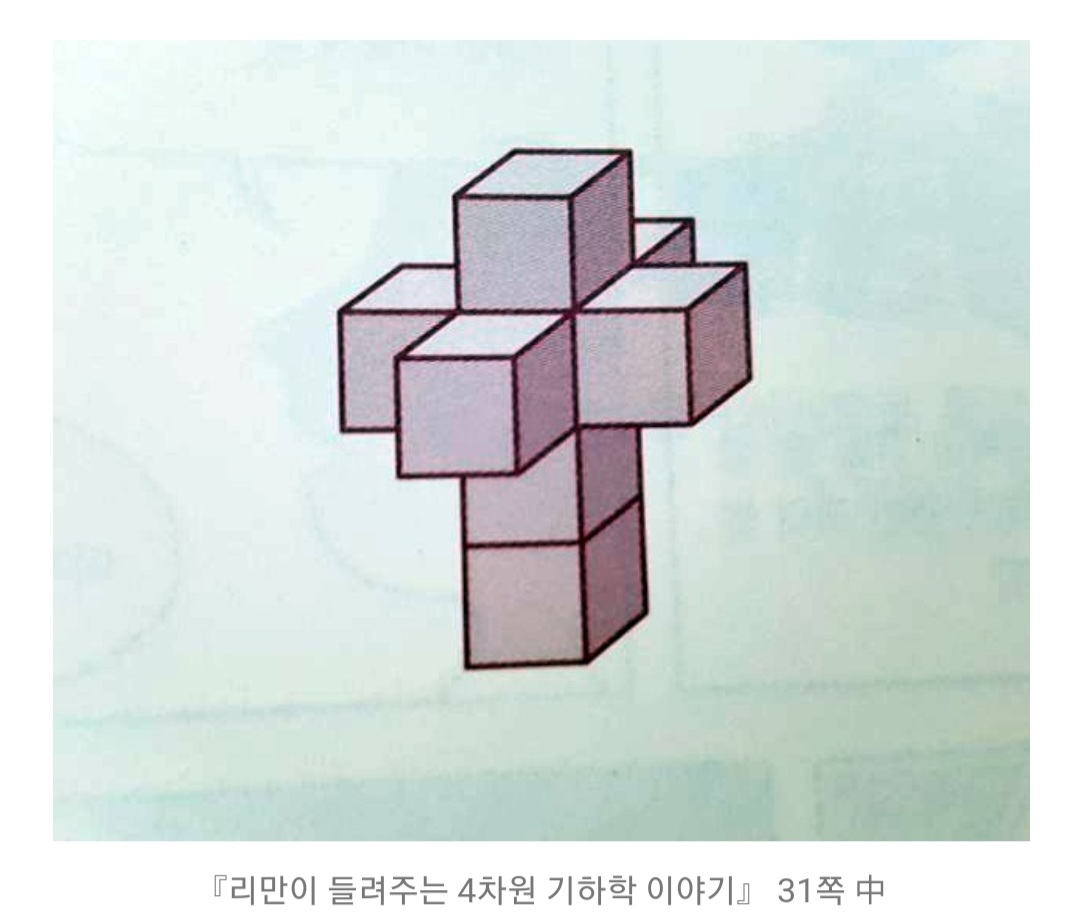
- 이제 현실 세계의 차원을 떠올려 보자. 만지면 입체감이 있고 보기에도 그렇지만, 과연 정말 3차원일까? 사실 우리는 현실 세계의 빛으로부터 눈 안쪽의 평평한 망막에 맺히는 2차원 정보를 볼뿐이다. 물체의 상은 평면이 되지만, 좌우 안구가 떨어진 만큼, 상의 어긋남을 바탕으로 깊이라는 정보가 추가된다. 즉, 우리가 3차원으로 보인다고 믿는 세상은, 실제로는 뇌에서 임의로 재구성한 가상의 3차원일 뿐이다. 그럼 세상이 사실 2차원인 것은 아닐까?
- 일단 3차원 세계에 살고 있다고 가정하고, 그보다 고차원일 경우도 알아보자. 만약 3차원의 구가 자기 세계로 2차원의 원을 데려가면, 과연 원이 그 세계를 이해할 수 있을까? 2차원 존재는 3차원 물체의 단면밖에 볼 수 없기에, 알고 있는 단어로 최선을 다해 보이는 것들을 설명한다 해도 제한적일 수밖에 없다. 그래서 우리도 스스로 설명할 수 있는 차원까지를 우리 세계라고 본다. 물론 여기에는 시간 차원이 빠져 있다. 우리가 4차원이라고 부르는 시공간은 3차원의 공간과 1차원인 시간 차원을 더한 것이다. 그런데 시간 차원은 왜 굳이 1차원일까? 시간 차원이 2차원 이상이라면 과거와 미래가 만나는 경우가 발생한다. 과거와 미래가 섞여 구분할 수 없어지므로, 당연하게 생각하던 인과관계가 전부 틀어지게 된다. 그래서 시간은 공간처럼 자유롭게 이동할 수 없고, 오직 하나의 방향을 가지며 한쪽으로만 이동할 수 있다. 이게 현재까지 우리 세계의 차원을 가장 정확하게 설명하는 내용이다.
- 직선의 정의가 차원에 따라 변한다는 사실을 인정하는 순간, 우리는 영원히 우주의 곡률을 구할 수 없게 되어버릴지도 모른다. 여전히 우주가 몇 차원인지조차 정확하게 모르는 슬픈 지적 생명체이기 때문이다. 그럼 어떻게 해야 할까? 아인슈타인은 우리가 사는 4차원 시공간이 과연 절대적인지 질문을 던졌다. 관측하는 사람의 관점에 따라 시공간은 늘어나거나 줄어든다. 이게 바로 상대성이론이다. 그리고 여기에는 다행히 어떠한 상황에서도 변하지 않는 빛의 속력이라는 하나의 절대적인 기준이 존재한다. 자연계에서 가장 중요한 건 두 점을 잇는 길이가 최소인 선이며, 진공 속의 빛은 일반적인 상황에서 흔들리지 않고 완벽한 직선을 표현할 수 있다. 그래서 천문학자들은 우주의 곡률을 구할 때, 우주배경복사 cosmic microwave background radiation라는 빛을 이용하며, 쉽지 않은 차원에 대한 이해도를 높이기 위해 멈추지 않고 여전히 노력하는 중이다.
- 수학 이론을 연구하는 것이 세상을 살아가는 데 쓸모없다고 말하는 사람도 있다. 하지만 상관없다. 수학자들은 그저 수학이 아름답고 경이롭기 때문에 하는 것이니까.
- 20세기 수학의 흐름을 바꾸었다고 평가받는 독일의 수학자 다비트 힐베르트는 칸토어를 지지했다. 심지어 그는 무한을 칸토어가 만들어 낸 '수학자들의 낙원'이라 표현하며, 무한의 특성을 쉽게 설명하기 위해 가상의 호텔을 하나 머릿속으로 지었다. 바로 무한한 객실을 보유한 힐베르트 호텔 Hilbert's Hotel이다. 이 호텔은 늘 객실이 손님으로 가득 차 있다. 그런데 재미있는 건, 새로운 손님이 몇 명이 오든 늘 빈방을 마련해 추가 손님을 묵게 할 수 있다는 것이다.
- 만약 특정한 인원이 아니라 무한 명의 손님이 와도 마찬가지다. 모든 방의 기존 손님들이 방 번호에 2를 곱한 방으로 옮기면, 무한한 홀수 번의 빈방이 생기니 신규 손님들은 순서대로 그 방으로 들어가면 된다. 무한 대의 버스를 타고 무한 명의 손님이 온다면 어떨까? 이럴 땐 1과 자기 자신으로만 나누어지는 수인 소수를 이용한다. 기존 손님은 소수 2에 자신의 방 번호를 제곱한 방으로 이동하고, 각각의 무한한 버스마다 3부터 이어지는 소수를 배정해서 무한한 손님들이 배정된 소수에 각자가 타고 온 버스 내에서 1번부터 차례로 부여받은 승차 번호를 제곱한 방으로 가도록 안내하면 끝이다. 아마도 빈방이 띄엄띄엄 많이 생기겠지만, 적어도 다른 호텔을 알아봐야 할 손님은 없을 것이다. (물론 매번 짐을 다시 싸고 풀어야 하는 손님들의 사정은 전혀 고려하지 않는 불친절한 호텔이긴 하다.) 이게 바로 무한이 가진 특별한 성질이다.
(리뷰자 주 : 2를 곱한 수는 자연적으로 모두 '합성수'로 변하게 된다. 따라서 각 버스에 2 이후의 소수인 3부터 소수를 부여함으로써 첫 번째(?) 무한은 해결된다. 이후 두 번째 무한인 승객들과 기존 손님들이 겹치지 않도록 하기 위해서는 각자 자신의 수를 제곱함으로써 -똑같아짐- 각각 2와 3 이상의 소수들이 곱해진 겹쳐지지 않는 각각의 무한 그룹으로 구분할 수 있게 된다.)
- 하지만 수학자들은 무한을 세는 방법을 알아냈고, 이젠 무한의 크기를 서로 비교도 할 수 있게 되었다. 무한이라는 난해한 표현을 이해하기 위한 무한한 접근을 해낸 것이다. 우리는 알아야 하며 알게 될 것이라던 힐베르트의 말처럼, 아무리 어려운 문제라도 인류는 반드시 명쾌한 결론에 도달할 수 있을 것이다. 정말 무한한 도전으로 말이다.
- 결국 완전무결함을 꿈꾸었던 유클리드도 실패자가 되어버린 걸까? 하지만 아인슈타인은 만일 자신이 과거의 기하학적 해석에 대해 몰랐다면 상대성이론을 결코 만들어 낼 수 없었을 것이라고 말했다. 일반 상대성이론은 공간에 대한 기반을 비유클리드 기하학 non-Euclidean geometry에서 가져온 것이며, 비유클리드 기하학 자체는 유클리드 기하학의 공리를 의심하는 과정에서 출발했기 때문이다.
- 과학은 진리가 아니다. 과학에서의 실패는 우리가 보편적으로 알고 있는 실패가 아닐 수도 있다. 결코 도달할 수 없는 목적지를 향해 무한히 접근해 가는 과정을 실패라고 한다면, 모든 실패는 또한 목적지로 오르기 위한 비상계단일 것이다. 결국 누구도 해보지 못한 시도를 하고, 그 안에서 완전히 새로운 방향을 찾는 것이 바로 과학에서의 숭고한 실패의 정의다. 과학은 실패를 위한 학문이며, 지금 우리가 누리는 모든 것도 끝없이 시도된 실패로부터 태어났다.
- 새롭게 정의된 관점에서 보면, 실패한 과학자들은 셀 수 없이 많다. 하지만 실패를 두려워한 과학자는 없었다. 심지어 그들 누구도 자신의 접근이 '실패'라고 생각하지 않았을 것이다. 과학에서 유일한 '실패'는 아무것도 시도하지 않는 상태이며, 혹시라도 '실패한 과학자들'이라고 불릴 만한 역사의 영웅들조차 새로운 통로를 열기 위해 힘차게 벽을 두드렸던 개척자들로 기억해야 한다.
- 혹시 지금 당신이 실패처럼 보이는 상황을 경험하고 있다면, 복잡하게 생각하지 말고 딱 한 가지만 기억하라. 우리가 누리는 모든 혜택이 얼마나 수많은 실패로부터 탄생한 멋진 성공인지를 말이다. 지금까지 과학은 언제나 우리가 붙잡고 버틸 수 있는 마지막 디딤돌이 되어주었고, 위기의 순간에서 항상 돌파구를 마련하는 놀라운 기적을 보여주었다.
- 절망적인 실패를 뛰어넘어 가장 경이로운 성공을 해낸 자기 자신의 위대함에 조금이라도 의심이 들거나 좀처럼 자부심이 느껴지지 않는다면, 그때야말로 두말할 나위 없는 과학이 등장할 좋은 순간이며, 절실하게 과학이 필요한 시간이다. 즐겁게 맞이해 주길 바란다.
- 영화 <나비 효과 The Butterfly Effect>로 널리 알려진 물리학 이론이 있다. 바로 카오스 이론 chaos theory이다. 1961년 미국의 기상학자 에드워드 로렌츠 Edward Lorenz는 컴퓨터로 미분방정식을 풀고 있었다. 컴퓨터가 출력된 결과를 다시 초기 조건으로 넣고 계산하는 과정을 지켜보던 그는, 시간을 아끼고자 예전에 적어둔 초기 조건을 손으로 입력했다. 그랬더니 놀라운 일이 벌어졌다. 그저 자동으로 입력되던 값을 직접 입력했을 뿐이었는데, 결과가 완전히 달라진 것이었다. 소수점 셋째짜리 미만의 미세한 오차가 문제였다. 컴퓨터가 입력할 때는 생략되지 않았던 매우 작은 숫자가 손으로 넣을 때는 삭제되었고, 그 결과 오차가 또 다른 오차를 낳는 과정이 연쇄적으로 일어나 예측하지 못한 값을 출력한 것이었다. 여기서 카오스 이론이 처음 등장했다. 이렇게 초기 조건에 민감해서 큰 차이를 갖는 결과를 도출하는 경우, 우리는 그 결과를 쉽게 예측할 수 없다.
- 여기에서 알파고는 몬테카를로 트리 탐색 Monte Carlo tree search이라는 방법을 활용했다. 갑자기 휴가를 떠나게 되었다고 하자. 여행 경비와 시간도 넉넉하게 주어지고, 원하는 곳이라면 어디라도 갈 수 있다. 이제 세계지도를 펼쳐 목적지를 골라야 하겠지만, 솔직히 모든 나라에 대한 정보를 알아도 정하기는 쉽지 않다. 그럼 어떻게 해야 할까? 보통 대표적인 관광지 몇 개만 뽑아 그중 하나로 정한다. 그리고 아마도 그 여행지는 적당히 마음에 들 것이다. 몬테카를로 트리 탐색이 바로 이런 원리다. 예상되는 수많은 경우의 수 중에서 임의로 몇 개만 뽑아 승률을 예측하기 때문에, 계산하는 시간을 효과적으로 줄여준다. 그럼 이세돌 9단과 알파고, 그 역사적인 대국의 결과는 어땠을까? 우리 모두가 알고 있듯이, 4승 1패로 알파고가 완승했다.
- 튜링의 삶은 아주 짧았지만, 한평생 여러 업적을 남겼다. 겉으로는 불규칙해 보이는 생명현상을 수학적으로 설명하는 일에도 관심이 많았다. 현대에는 이러한 분야를 '수리 생물학 mathematical biology'이라고 부른다. 튜링은 표범의 점무늬나 얼룩말의 줄무늬를 관찰하며 동물마다 다른 무늬를 가지는 이유에 대해 호기심을 느꼈고, 무늬를 형성하는 성분과 억제하는 성분의 상호작용을 간단한 방정식으로 정리했다. 생물학적인 진화의 메커니즘을 자신만의 독창적인 수학적 방식으로 기술하고자 시도한 것이다.
- "우리는 단지 아주 가까운 곳까지만 볼 수 있을 뿐이지만, 그 안에서도 우리가 해야 할 일을 충분히 많이 찾을 수 있다"라고 말하던 앨런 튜링이야말로, 아주 짧은 시간 동안 보이는 모든 곳에서 스스로 할 수 있는 일을 찾아 모두 해내고야 만 수학자가 아닌가 싶다. 그의 정신 역시 누군가가 함부로 판별할 수 없는 명제처럼 복잡하지만 결코 멈추지 않고 영원히 이어질 것이다.
- 특히, 계산할 거리가 쌓여만 가던 과학자들은 고민이 많았다. 처리 속도가 너무 느리다 보니 연구를 빠르게 진척시킬 방법이 필요했고, 그래서 나온 것이 바로 슈퍼컴퓨터다. 컴퓨터의 성능은 플롭스 FLOPS, floating point operations persecond라는 단위를 사용해 나타내는데, 이는 1초 동안 수행할 수 있는 부동소수점 연산 횟수를 말한다. 컴퓨터는 모든 언어를 0과 1, 두 가지로만 이해하는 2진법을 사용하기 때문에, 우리가 쓰는 10진법의 모든 숫자를 단 두 가지의 숫자로만 표현해야 한다. 하지만 변환하는 과정에서 무한하게 순환하는 수가 되어버리는 경우가 있기 때문에, 이것을 근사하는 과정에서 소수점의 위치를 고정하지 않고 그 위치를 나타내는 수를 따로 적게 된다. 이렇게 하면 컴퓨터가 10진법을 이해하기가 편해지며, 이걸 빨리해야 컴퓨터가 버벅거리지 않게 된다.
- 가장 친숙한 반려동물 중 하나인 개의 나이를 사람 나이로 환산하려면, 흔히 개의 나이에 7을 곱한다고 알려져 있다. 세 살이 된 개는 인간으로 치면 21세 정도며, 개가 만약 열두 살이라면 84세의 노인과 비슷한 나이라는 말이다. 하지만 2019년에 미국 과학자들은 DNA 메틸화를 적용해 새로운 나이 환산법을 만들어 냈다. 그 결과, 개는 어릴 때 사람보다 훨씬 빠르게 성장하고, 나이가 들면 들수록 천천히 늙는 것으로 밝혀졌다. 개가 세 살이면 이미 40대 후반이지만, 열두 살이라고 해도 인간으로 치면 70세 정도라는 것이다. 개뿐만 아니라 사람도 얼마나 늙었는지를 이렇게까지 정밀하게 추정할 수 있다면, 남아 있는 수명을 알아내는 것도 문제없을 것이다. 물론 질병이나 사고 등 외부 요인으로 인한 변수는 배제해야 한다. 오스트레일리아의 과학자들은 척추동물 252종의 유전자 정보를 분석한 결과, 최종적으로 인간의 자연 수명이 38년이라는 결과를 얻었다.
- 혹시 죽음의 순간에 쥐가 기억을 회상하는 건 아닐까 하는 추측이 제기되었지만, 이를 곧바로 인간과 성급하게 연결 지을 수는 없었다. 그러다가 2022년 2월, <죽어가는 인간의 뇌에서 신경세포 일관성 및 결합의 향상된 상호작용 Enhanced Interplay of Neuronal Coherence and Coupling in the Dying Human Brain>이라는 주제의 논문이 발표되었다. 논문에는 환자를 치료하는 과정에서 우연히 발견하게 된 내용이 담겨 있다. 어느 날 87세 남자가 뇌출혈이 발생해 병원 응급실에 도착했는데, 뇌전증 발작이 감지되어 바로 뇌파 검사를 진행하게 되었다. 안타깝게도 환자는 그 도중 심장마비로 유명을 달리하게 되었지만, 심장박동이 멈추기 전과 후 약 30초 동안 일어난 뇌 활동을 기록할 수 있었다. 다양한 활동 중에서도 주로 관측된 뇌파는 기억을 회상하거나 고차원적인 인지 정보를 처리할 때 나타나는 감마파였다. 물론 단 한 번의 사례만으로 무조건 죽음 직전에 과거를 떠올린다고 단정 지을 수는 없겠지만, 쥐 실험과 연결 지을 만한 후속 연구가 처음으로 등장했다는 점에서 의미 있는 결과였다.
- 1875년 영국의 생리학자 리처드 케이턴 Richard Caton은 토끼와 원숭이의 뇌에서 검출한 파형을 검류계에 기록했다. 아마도 최초의 뇌파를 발견한 사례이리라. 그로부터 50년쯤 지나 1924년에는 독일의 신경과학자 한스 베르거 Hans Berger가 세계 최초로 뇌파를 기록하는 장치를 개발했는데, 그가 뇌파를 연구하게 된 계기가 재미있다. 그는 군대에 있을 때 달리는 말에서 떨어지는 사고를 당했는데, 공교롭게도 마침 동생이 멀리서 전보를 보내 베르거의 안부를 물었다. 자신이 다쳤다는 소식이 전달될 만한 시간적 여유가 없었기에, 베르거는 묘한 호기심이 들었다. 위기의 순간에 무언가 알 수 없는 방법으로 멀리 떨어져 있는 동생에게 어떤 신호가 전달된 건 아닐까? 말하지 않고도 정보를 전달할 방법이 있을지도 모른다고 생각했던 그는 그 뒤로 뇌파 연구에 매진하게 되었다.
- 언젠가 죽음의 순간이 왔을 때, 생존을 위해 격렬하게 과거의 기억을 더듬어 나가는 뇌와 그로 인해 발생하는 복잡한 뇌파를 떠올리면 슬프고 처량해진다. 하지만 다시 생각해 보면, 마지막 숨을 몰아쉬기 직전까지 우리가 살아온 나날들을 뒤돌아 보는 기회를 제공해 주는 뇌의 마지막 노력이 숭고하게 다가온다. 죽음에 이르기 전 뇌가 정말로 과거 기억을 회상하는지는, 가까운 시일에 뇌파와 관련된 완벽한 실험 결과와 사례 들이 등장하면서 정리될 것이다. 하지만 그 행위가 정말로 생존을 위한 마지막 몸부림인지, 아니면 후회 없는 삶을 돌아보기 위한 찰나의 여운인지는 영원히 알 수 없을 것이다.
(리뷰자 주 : 개인적으로는 세이브와 연결 지어 생각하고 있다.)
- '커 블랙홀'이라고 이름 붙였다. 거대한 수박 두 통처럼 생긴 2개의 별 중 한 녀석이 블랙홀로 변하면, 나머지 녀석의 물질은 청소기의 전원 코드 선이 감길 때처럼 뱅뱅 돌면서 옆 친구에게 빨려 들어간다. 그 과정에서 마치 레코드판 모양으로 블랙홀 주변을 감싸게 되는데, 이걸 '강착원반 accretion disk'이라고 부른다. 그리고 서로 빨려 들어가려고 물질들끼리 싸우다 보면, 마찰로 인해 에너지가 방출된다. 우리는 이 에너지를 관측해 비로소 블랙홀의 존재를 확신할 수 있었다. 클럽 디제이의 디스크처럼 멋지게 돌아가는 블랙홀의 모습이 궁금하다면, 영화 <인터스텔라 Interstellar>에서 만나볼 수 있다. 물론 영화에 등장하는 블랙홀, 가르강튀아를 비롯해 그전까지 봐왔던 모든 블랙홀은 그저 상상을 기반으로 만든 이미지일 뿐이었다. 이제 인류는 블랙홀의 직접적인 관측을 꿈꾸게 되었다.
- 뜨거운 해가 지고 선선한 바람이 부는 하늘이 어둠으로 물들면, 북쪽 밤하늘에 귀여운 녀석이 풀어헤친 머리를 들이민다. 맨눈으로도 보이는 외로운 우주의 여행자, 니오와이즈 혜성이다. 이 녀석을 처음 발견한 우주망원경 니오와이즈 NEOWISE의 이름을 따서 부르기는 하지만, 정식 명칭은 'C/2020 F3'이다. 이 복잡한 이름은 어디서 왔을까. 우선 맨 앞의 'C'는 다시 돌아오는 혜성의 주기가 200년이 넘어, 앞으로 우리의 남은 일생 동안 다시 만날 수 없다는 말이다. 그보다 짧은 주기라 또 볼 가능성이 있으면 'P'를 붙여준다. 바로 그다음에 오는 숫자와 문자는 발견된 시기와 순서다. 1년을 24등분한 뒤, 구간별로 알파벳을 붙이면 F는 여섯 번째 구간이 된다. 결과적으로 니오와이즈 혜성은 2020년 3월 중순 이후에 세 번째로 발견된 장주기 혜성이라는 걸 알 수 있다. 그리 중요하진 않지만, 간단한 암호 해독에 성공한 셈 치자.
- 혜성 역시 소행성처럼 태양 곁을 돌고 있기는 하지만, 매우 길쭉한 타원궤도를 그린다. 주성분이 얼음과 먼지라, 가끔 태양 근처를 지나가며 표면의 얼음이 녹으면서 궤도 위에 먼지를 흩뿌린다. 이게 바로 하얗고 밝게 빛나는 혜성의 먼지 꼬리다. 사실 꼬리가 하나 더 있는데, 태양에서 나온 입자들인 태양풍이 혜성에 부딪혀서 만들어진 것이다. 이때 발생한 고에너지의 이온들은 다시 태양풍이 흘러가는 대로 따라간다. 그래서 태양이 있는 방향과 정반대의 방향으로 뻗어나가는 푸른 꼬리가 생기는데, 이를 '이온 꼬리 ionic tail'라고 부른다. 맨눈으로는 먼지 꼬리가 훨씬 잘 보이긴 하지만, 어느 쪽이든 실제로 보는 것은 꿈만 같은 일이다.
- 다섯 은하가 모여 '스테판의 오중주 Stephan's Quintet'라 불리는 지역도 놀라움을 금할 수 없었다. 1787년에 발견된 은하군에는, 1개의 은하가 그 뒤의 4개의 은하들과 달리 그들과 완전히 동떨어져 있다는 놀라운 비밀이 숨겨져 있다. 네 친구가 사진을 찍는 도중 길을 가던 다른 친구가 우연히 카메라에 들어온 상황이다. 엄청난 해상도를 지닌 제임스 웹 우주망원경은 은하들이 활발하게 서로 끌어당기며 상호작용 하는 놀라운 모습을 섬세하게 잡아냈다.
- 마지막 사진은 찬란한 별의 탄생을 보여주는 카리나 성운 Carina Nebula이다. 일종의 거대한 우량아 별 산후조리원이라고 볼 수 있으며, '용골자리 성운 NGC 3324'이라고도 불린다. 위쪽에 존재하는 젊은 별들이 내뿜는 복사에너지로 인해 먼지와 가스가 아래쪽으로 밀려나면서 마치 거대한 산맥과 같은 모습을 보이는데, 심지어 먼지로 만들어진 봉우리 안쪽까지 자세히 보여서 마치 요람에서 배냇저고리로 꽁꽁 감싸고 있던 아이의 고사리손과 얼굴을 처음 확인하는 것과 같은 환상적인 순간을 선보인다.
- 1827년에 촬영된 세계 최초의 사진 <그라의 창문에서 바라본 조망 Point de vue du Gras>을 찍기 위해 니엡스라는 사진가는 장장 8시간 동안 상을 고정하고 기다렸다. 우리는 최종 보정이 끝난 결과물만 보기에 별다른 차이를 느끼지 못할 수도 있지만, 실제로는 그사이 엄청난 혁신이 일어났다. 지금은 한 장의 사진을 얻기까지 1초도 걸리지 않는다.
- 블랙홀은 모든 정보를 흡수해서 전부 똑같이 만들어 버릴지도 모른다. 즉, 정보를 파괴하며, 정보는 파괴될 수 없다는 명제마저 함께 파괴해 버릴지도 모른다. 블랙홀 안으로 들어가거나 블랙홀이 방출하는 물질을 모두 모아서 분석하는 것은 현실적으로 불가능하기에, 서로 다른 견해를 갖고 있던 과학자들은 싸우기 시작했다. 호킹과 <인터스텔라>로 유명한 킵 손은 블랙홀에 들어간 정보는 파괴되어 회수할 수 없기에, 역설은 근본적으로 해결될 수 없다고 주장했다. 반대 진영에는 캘리포니아 공과대학교의 물리학자이자 내기의 달인 존 프레스킬 John Preskill이 있었다. 사건의 지평선의 내부와 외부에 관측자가 동시에 존재할 수 없다는 상보성 때문에, 아무도 두 가지 상황을 동시에 볼 수 없으니 모순이나 역설은 없다는 것이 그의 논리였다. 호킹은 우리가 알 수 없으니 정보 역설이 풀렸다고 인정했지만, 킵 손은 패배를 인정하지 않았다.
- 이후 끈 이론 string theory으로 블랙홀을 설명하는 퍼지볼 fuzzball 가설이나, 사건의 지평선 대신 방화벽을 세우는 블랙홀 방화벽 역설 등 다양한 견해가 등장했다. 심지어 헤어진 연인의 사진이 담긴 디지털카메라가 고장이 나서 사진을 꺼낼 방법이 없는 것처럼 정보는 사라지지 않았지만 영원히 꺼낼 방법이 없다는 주장까지 나왔다. 몇몇 과학자들은 정보가 블랙홀 안으로 절대 들어갈 수 없다고 주장했는데, 그렇게 탄생한 게 바로 홀로그램 우주 가설이다. 블랙홀 바깥에서 보았을 때 정보가 블랙홀의 경계에 붙어 있을 뿐이며, 블랙홀 안에서 파괴되지 않고 단지 사건의 지평선 표면에 암호화되어 기록된다면 어떨까? 블랙홀의 질량이 증가할수록 사건의 지평선도 커지기에, 정보를 기록하고 보존할 수 있는 공간도 함께 늘어난다는 원리다.
- 우주는 어떻게 만들어졌을까? 신비로운 맛집의 비밀을 밝히려면 들어가는 재료 하나하나를 알아내야 하는 것처럼, 우주를 설명하기 위해서는 우주를 이루는 모든 재료를 정확하게 이해해야 한다. 인류가 지금까지 발견한 모든 재료를 '기본 입자 standard modet'라 하며, 이들과 이들 사이의 상호작용을 설명하는 형태가 바로 표준 모형 standard model이다. 오랫동안 과학자들의 임원은 이걸 다듬고 완성하는 것이었다. 그리스의 철학자 엠페도클레스는 세상의 모든 만물이 흙, 불, 공기, 물로만 이루어져 있다는 4원소설을 주장했지만, 이들은 모두 원자로 이루어진다. 원자의 중심에는 원자핵이 있고 그 주위에는 전자가 있다. 원자핵은 양성자와 중성자로 구성되어 있으며, 이들은 다시 업 쿼크와 다운 쿼크로 쪼개진다. 중성자보다 더 작아서 '중성미자 neutring'라고 불리는 녀석도 있는데, 질량이 너무 작아서 측정하기도 어렵다. 업 쿼크, 다운 쿼크, 전자 그리고 중성미자, 여기까지가 현대판 4원소설이다. 만약 이 우주가 오직 네 종류의 치킨으로만 이루어져 있다면, 우리는 프라이드, 양념, 간장, 마늘 치킨을 찾아낸 것이다. 이것이 1세대 기본 입자인데, 현재까지 발견된 세대는 총 3세대다. 2세대와 3세대 역시 1세대처럼 네 가지 기본 입자로 구성되어 있다. 각운동량이나 스핀 spin은 같지만, 질량이 다르다. 이제 단순한 4치킨의 시대는 끝나고, 핫양념, 볼케이노, 숯불양념, 강정, 왕갈비, 불갈비, 베이크, 가마솥 치킨까지 더해 12치킨의 시대가 온 것이다. 이 열두 가지 기본 입자를 우리는 '페르미온 fermion'이라고 부른다.
- 우주에는 네 가지 힘, 즉 중력, 전자기력, 강력, 약력이 있다. 현대물리학에서는 이 힘들의 근원을 주고받는 입자로 설명한다. 배구공을 주고받는다면 배구를 하고 있다고 보는 것처럼, 두 입자가 서로 광자, 글루온, Z 보손, W 보손과 같은 매개 입자를 주고받는 과정에서 힘이 생긴다고 본다. 이들을 '보손 boson'이라 하는데, 열두 가지 치킨을 '페르미온'이라고 부르는 것처럼, 네 종류의 디핑 소스인 허니머스터드, 치즈, 와사비마요, 갈릭 소스가 바로 보손이다. 그런데 이상하게도 이들의 질량은 모두 다르다. 우주를 이루는 입자들에는 도대체 누가 질량을 부여했을까?
- 2011년 12월, 힉스 입자가 없다면 나타나야 할 형태와 조금 다른 결과가 나왔다. 아무 소리도 나지 않아야 할 빈 깡통 속에서 뭔가 달그락거리는 소리가 들린 것이다. 과학자들은 잘못된 신호일 거라며 믿지 못했다. 하지만 그들은 수개월간 분석을 멈추지 않았고, 2013년 3월 14일, 그 존재의 가능성이 제시된 지 49년이 지나서야 드디어 미지의 입자가 세상에 모습을 드러냈다. 이제 인류는 입자에 질량을 부여하는 힉스장과 힉스 메커니즘, 그리고 그 증거인 힉스입자의 존재를 받아들이게 되었다.
- 프랑스의 오리엔탈리즘 화가 장 레옹 제롬의 그림 <아레오파고스 앞의 프리네 Phryne before the Areopagus>라는 작품이 있다. 아레스 신의 바위라는 뜻의 ‘아레오파고스’는 고대 아테네의 정치 기구로 법정처럼 범죄자에 대한 재판을 여는 역할도 했기에, 다른 표현으로 바꾸면 '배심원 앞에 선 프리네’가 된다.
(리뷰자 주 : 나는 이 사건의 핵심은 '왜' 프리네가 배심원 앞에 서야 했는가라고 본다. 답은 질문에 따라 결정된다.)
- 먼저 끈 이론과 초끈 이론에 대해 짚고 넘어가자. 둘의 차이를 설명하기 위해서는, 페르미온과 보손부터 알아야 한다. 우주를 구성하는 열두 가지 기본 입자를 페르미온이라고 부르며, 이런 입자들이 배구를 하듯이 공을 주고받으며 우주에 존재하는 힘을 만들어 낸다. 여기서 배구공의 역할을 하는 매개 입자가 보손이다.
- 우주의 네 가지 힘 가운데 벌써 세 가지나 합친 것이다. 하지만 여전히 표준 모형은 중력을 포괄할 수 없다는 한계를 갖고 있다. 하지만 초끈 이론을 사용하면 표준 모형의 근간인 양자역학을 중력에 적용할 수 있게 된다. 다만 끈을 양자화하기 위해서는 중력자가 존재해야 하는데, 아직 중력자는 관측되지 않고 있다. 미국의 페르미국립가속기연구소나 유럽입자물리연구소 등에서도 중력자가 여분의 차원으로 이동하는 순간을 관측하기 위해 노력하고 있지만, 현재 인류가 보유한 지식수준으로는 접근 불가능한 영역에 있는지도 모른다.
- 양자 세계가 갖는 물리적 성질 중에 불확정성 원리가 있다. 입자의 위치와 운동량을 정확하게 관측할 수 없다는 말이다. 관측 장비의 한계 때문이 아니다. 원리적으로 그렇다. 그런데 재미있는 건 끈 속에서 불확정성 원리 때문에 양자 요동이 일어나면 끈의 진동 패턴이 그만큼 상쇄되고, 상쇄되고 남은 값은 기본 입자의 질량과 정확하게 맞아떨어진다는 것이다. 심지어 아직 발견하지 못한 중력자의 경우는 완벽히 상쇄되어 질량이 0이 된다. 아침에 급하게 외출하며 지폐와 동전들을 한 움큼 집고 나왔는데, 종일 사용한 돈과 1원의 차이도 없이 깔끔하게 맞아떨어져 빈손으로 귀가하는 셈이다. 우연의 일치라고 해도 수학적으로 너무 아름답다. 그러니 이런 아름다움에서 빠져나가지 못한 학자들이 끈 이론에 집착할 수밖에 없다.
- 영국의 수학자 앤드루 와일스 Andrew Wiles는 열 살 무렵 하굣길에 지역 도서관에 우연히 들렀다가 페르마의 마지막 정리를 발견하고 완전히 매료당했다. 이후 이 정리를 증명할 기회만 엿보며, 꾸준히 수학자의 길을 걸었다. 하지만 그의 지도교수 역시 증명이 불가능해 보이던 페르마의 마지막 정리 대신, 당시 그것과 전혀 관계없어 보였던 타원곡선을 그에게 전공으로 추천했다. 행운이란 준비가 기회를 만났을 때 나타난다. 놀랍게도 페르마의 마지막 정리와 가장 밀접한 것이 바로 그의 전공이었던 타원곡선이었다. 물론 결코 쉬운 일은 아니었다. 당근이 당근 케이크로 바뀌었지만, 무한개의 당근 케이크가 전부 존재하지 않는다는 것을 밝혀내야만 했다. 검토 과정에서 문제점이 발견되기도 했지만, 와일스는 1년이 넘는 은둔 생활 끝에 더욱 간결한 증명을 해냈다. 비록 완벽한 증명은 아니었지만, 전설적인 난제를 정복하기에는 충분했다. 볼프스켈상 역시 90년 만에 주인을 찾게 되었다.
- 페르마의 마지막 정리가 증명되자 수학자들은 행복해했을까? 그들은 기뻐하기는커녕 오히려 목표를 잃었다고 좌절했다. 와일스는 페르마의 마지막 정리를 증명한 이후 새 문제 만들어 달라는 부탁에 시도 때도 없이 시달리게 되었다. 그래서 탄생한 것이 바로 밀레니엄 7대 난제로, 수학자들은 유일하게 증명된 푸앵카레 정리를 제외한 나머지 6개의 난제에 여전히 즐거운 마음으로 도전하고 있다. 페르마의 마지막 정리에 관한 이야기는 여기까지다.
- 1884년, 영국 빅토리아 시대의 언어학자이자 신학자인 에드윈 애보트 Edwin Abott는 최초의 SF 소설 <플랫랜드 Flatland>를 대중에게 선보였다. '다차원의 로맨스 Romance of Many Dimensions'라는 부제가 붙었던 이 소설은 정사각형이 경험한 3차원 세상에 대한 수기다. 간단한 말해, 납작한 2차원 세상에서 살아온 존재가 3차원 세상을 접하고 나서, 다시 돌아와 자신의 경험담을 말하다가 불온한 사상을 전파한다는 이유로 종신형을 선고받는다는 이야기다. 그만큼 차원에 대한 개념은 설명하기가 쉽지 않고, 누구에게도 이해시킬 수 없다는 말이다.
- 미국의 위대한 과학 소설가 아이작 아시모프 Isaac Asimov는 이 책의 미국판 서문에서 다음과 같이 평가했다. "우리가 아는 한, 공간의 여러 차원을 인식하는 방법을 가장 잘 소개한 작품이며, 단순히 기하학의 지식을 재치 있고 재미있게 다룬 것이 아니라, 우리의 우주와 우리 자신에 대한 깊이 있는 사색까지 담고 있는 한 편의 학위논문과 같은 소설이다."
- 2000년, 다가오는 21세기를 한껏 기대하던 수학자들은 뭔가 재미있는 이벤트 같은 게 없을까 고민하다가 수학계에서 가장 중요하고 어려운 문제 7개를 뽑기로 했다. 나비에-스토크스 방정식의 해의 존재와 매끄러움, 리만 가설, 버츠와 스위너톤-다이어 추측, 양-밀스 가설의 존재와 질량 간극, 호지 추측, P-NP 문제, 그리고 푸앵카레 추측. 왠지 외워두면 언젠가 명절에 퀴즈쇼를 보다가 아는 척할 기회가 한 번쯤은 올 것 같지만, 그러기엔 뇌 용량이 아까울 수도 있다. 중요한 건 이 중에 풀린 문제가 딱 하나 있다는 것이다. 바로 푸앵카레 추측이다.
- 세계 최고의 수학자들에게 3단 고음 수준의 3단 낙담을 안겨준 페렐만은 천재 수학자 레온하르트 오일러의 도시, 상트페테르부르크에서 태어났다. 박사를 마치고 스탠퍼드, 프린스턴 등 유명 대학교에서 초청을 받았지만 거절하고, 수학 말고 다른 건 하지 않겠다는 일념으로 고향인 상트페테르부르크 스테클로프 수학연구소 Steklov Institute of Mathematics로 진로를 결정했다. 1996년 유럽수학회상도 자신의 연구가 완성되지 않았다는 이유로 거절했다.
- 현재 그는 어머니와 단 둘이 작은 아파트에서, 나라에서 주는 실업수당으로 끼니를 때우며 4차원에 존재하는 형태들은 모두 몇 개인지 찾는 것으로 알려졌다. 그저 원해서 공부했고, 그래서 연구했을 뿐인 페렐만은 유명해지고 싶은 마음은 전혀 없고, 오직 연구만 하고 싶었던 것이다. 그리고 그 이유는 처음 추측을 제시한 푸앵카레의 말속에서 찾을 수 있다. "과학자가 자연을 연구하는 이유는 쓸모 있기 때문이 아니라 아름답기 때문이다. 만약 자연이 연구할 가치가 없다면, 우리의 인생 또한 살 가치가 없을 것이다."
- 당연히 자연수가 홀수보다 많을 것 같다. 과연 그럴까? 두 수는 모두 무한하다. 그럼 이제 사탕을 세는 방식을 똑같이 써보자. 자연수와 홀수를 하나씩 짝을 지어서 세는 것이다. 어떻게 짝을 지어도 남거나 모자라는 수는 존재하지 않는다. 즉, 자연수와 홀수의 개수는 서로 같다는 말이다. 그래서 칸토어는 무한의 경우에는 전체와 그 일부가 같다는 결론을 내렸다. 무한을 인정하지 않았던 그의 지도교수는 훗날 그가 교수직에 임용되지 못하도록 손썼고, 천재 수학자 앙리 푸앵카레도 무한에 대한 그의 집착을 질병이라며 비판했다. 그는 우울증에 시달렸고, 결국 정신병원에서 생을 마감했다.
'활자가 흐르는 이야기 > Book(~2024)' 카테고리의 다른 글
| [이석원] 2인조 - 우리는 누구나 날 때부터 2인조다 (0) | 2022.11.27 |
|---|---|
| [박세니] 어웨이크 - 내 안에 잠든 무한한 가능성을 깨워라 (0) | 2022.11.26 |
| [빅터 프랭클] 죽음의 수용소에서 - 죽음조차 희망으로 승화시킨 인간 존엄성의 승리 (0) | 2022.11.20 |
| [알렉산더 케이] 네가 세계의 마지막 소년이라면 (2) | 2022.11.01 |
| [도스토옙스키] 지하로부터의 수기 (0) | 2022.10.31 |
| [태지원] 그림으로 나를 위로하는 밤 - 지친 마음에 힘이 되어주는 그림 이야기 (0) | 2022.10.30 |